Distribuciones Continuas
Distribución Gamma
Algunas variables aleatorias son siempre no negativas y por varias razones dan distribuciones de datos que están sesgadas (no simétricas) a la derecha.
Esto es, casi toda el área bajo la función de densidad está ubicada cerca del origen y lafunción de densidad cae gradualmente conforme y aumenta.
Imagine una variable aleatoria distribuida como Poisson con parámetro \(\lambda\), por ejemplo, el número de correos electrónicos que llegan a su bandeja de entrada en una semana, o el número de carros que entran al parqueo de ciencias económicas en un día. Ahora, hay una manera alternativa de definir el proceso: pensar en el tiempo que pasa entre lallegada de un correo (o un carro) y otro. Este tiempo se puede definir como una variable aleatoria i.i.d. Exponencial con parámetro \(\lambda\).
Distribución Gamma
Entonces, la suma de \(n\) de estos tiempos nos daría el tiempo para la \(n\) -ésima llegada (el tiempo para que el n-ésimo correo llegue o para que el \(n\)-ésimo carro llegue), y como veremos más adelante, la suma de v.a. que son iid Exponenciales es una v.a. distribuida como \(Gamma(n, \lambda)\).
Estos intervalos de tiempo entre eventos (correos, carros, etc.) poseen una distribución de frecuencia sesgada, al igual que los intervalos de llegada en una fila de espera en las cajas de un supermercado (esto es, la fila de espera para llegar a la caja a pagar). La población asociada con estas variables aleatorias posee con frecuencia funciones de densidad que son modeladas de manera adecuada por una función de densidad \(Gamma(n, \lambda)\).
Distribución Gamma
Se dice que una variable aleatoria \(X\) tiene distribución de probabilidad Gamma con parámetros \(\alpha > 0\) y \(\beta > 0\) si y solo si su función de densidad es:
\[ f_X(x)= \begin{cases} \dfrac{x^{\alpha-1} e^{-x/\beta}}{\beta^{\alpha}\Gamma(\alpha)}, & 0 \le x < \infty, \\[6pt] 0, & \text{en otro caso.} \end{cases} \]
donde la función Gamma está dada por:
\[ \Gamma(\alpha)=\int_{0}^{\infty} x^{\alpha-1} e^{-x}\,dx. \]
Distribución Gamma
Importante: la Función Gamma NO es lo mismo que la Función de Densidad Gamma (aunque esta última incluye a la primera).
- En inglés: http://mathworld.wolfram.com/GammaFunction.html
- En español: https://es.wikipedia.org/wiki/Funci%C3%B3n_gamma
Igualdades útiles de la Función Gamma
- \(\Gamma(z) = (z - 1)! \quad \text{para } z \in \mathbb{Z}\)
- \(\Gamma(z + 1) = z \, \Gamma(z)\)
- \(\Gamma(1) = 1\)
- \(\Gamma(1 - z)\Gamma(z) = \dfrac{\pi}{\sin(\pi z)}, \quad \text{donde } z \notin \mathbb{Z}\)
- \(\Gamma\!\left(\tfrac{1}{2}\right) = \sqrt{\pi}\)
Distribución Gamma
library(ggplot2)
set.seed(123)
n <- 100000
df <- data.frame(vargamma = rgamma(n, shape = 1, scale = 1))
ggplot(df, aes(x = vargamma)) +
geom_histogram(aes(y = after_stat(density)),
bins = 30, fill = "grey70", color = "black") +
stat_function(fun = dgamma, args = list(shape = 1, scale = 1),
linewidth = 0.9, color = "darkgreen") +
coord_cartesian(xlim = c(0, 10), ylim = c(0, 1)) +
labs(
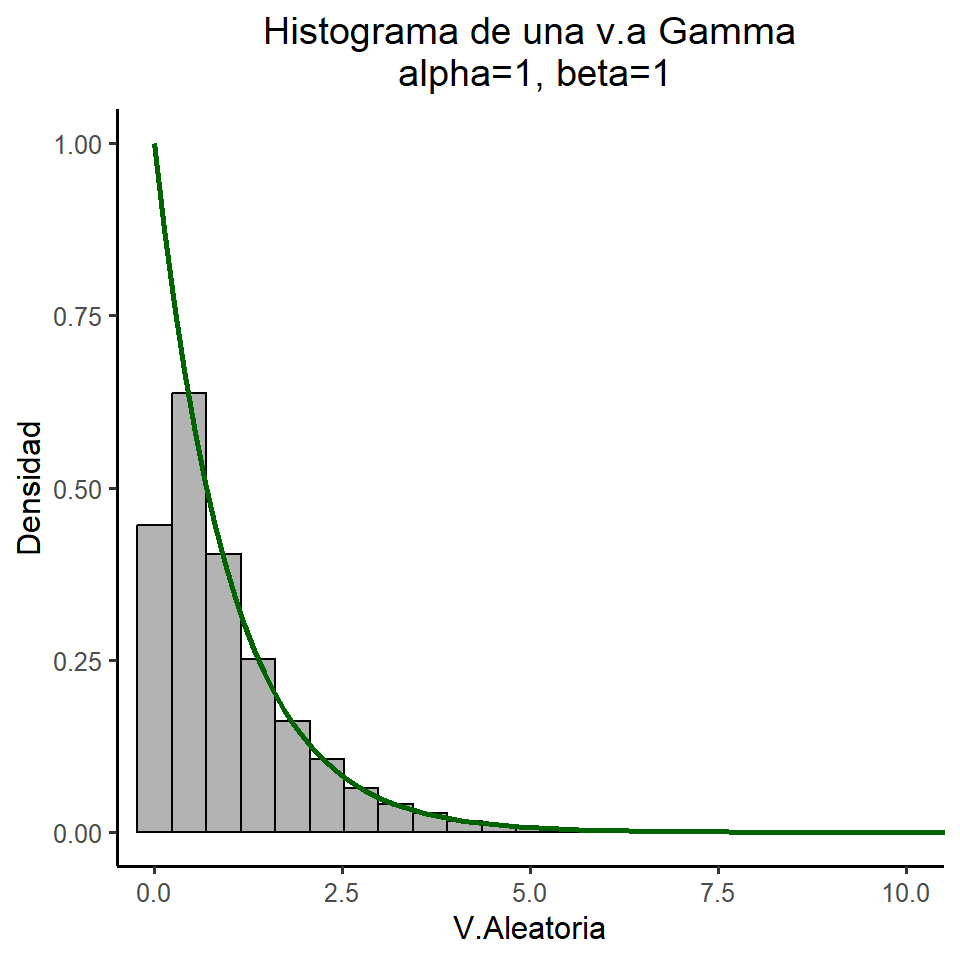
title = "Histograma de una v.a Gamma\ncon alpha=1, beta=1",
x = "V.Aleatoria", y = "Densidad"
) +
theme_classic(base_size = 12) +
theme(plot.title = element_text(hjust = 0.5))Distribución Gamma
library(ggplot2)
set.seed(123)
n <- 100000
df <- data.frame(vargamma = rgamma(n, shape = 4, scale = 1))
ggplot(df, aes(x = vargamma)) +
geom_histogram(aes(y = after_stat(density)),
bins = 30, fill = "grey70", color = "black") +
stat_function(fun = dgamma, args = list(shape = 4, scale = 1),
linewidth = 0.9, color = "darkgreen") +
coord_cartesian(xlim = c(0, 10), ylim = c(0, 1)) +
labs(
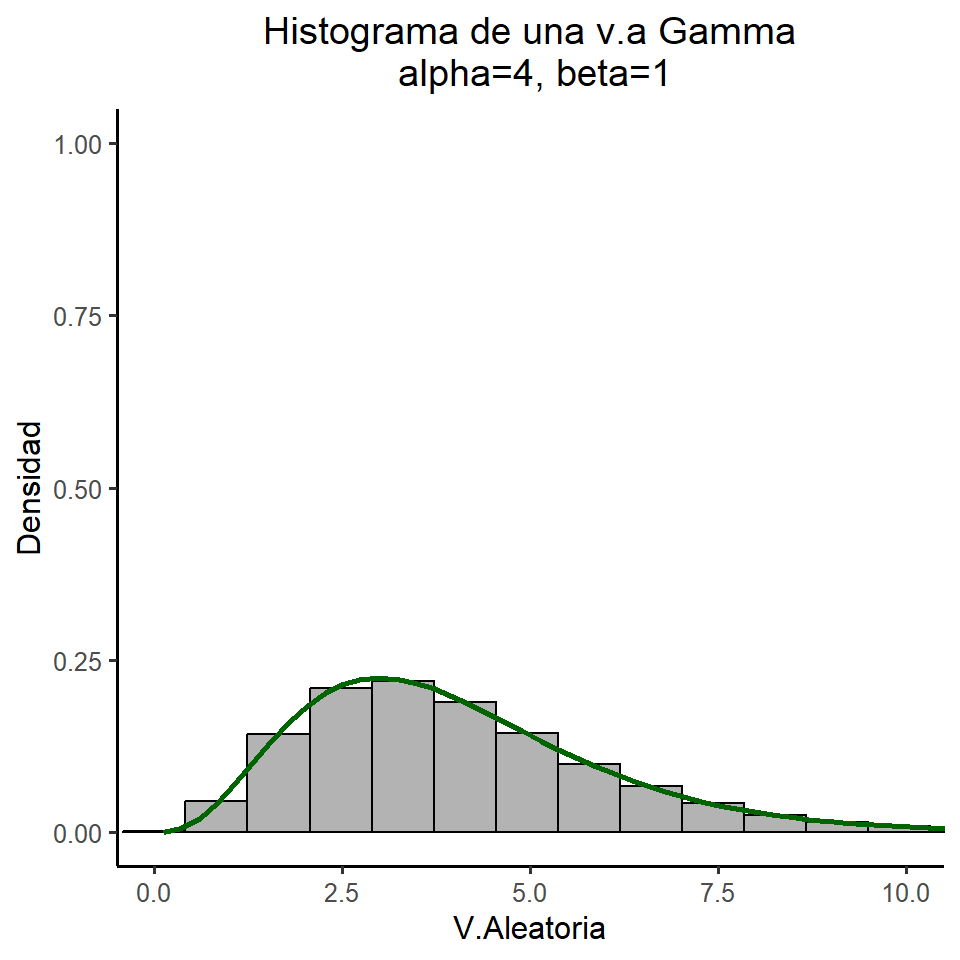
title = "Histograma de una v.a Gamma\ncon alpha=4, beta=1",
x = "V.Aleatoria", y = "Densidad"
) +
theme_classic(base_size = 12) +
theme(plot.title = element_text(hjust = 0.5))Distribución Gamma
library(ggplot2)
set.seed(123)
n <- 100000
df <- data.frame(vargamma = rgamma(n, shape = 9, scale = 1))
ggplot(df, aes(x = vargamma)) +
geom_histogram(aes(y = after_stat(density)),
bins = 30, fill = "grey70", color = "black") +
stat_function(fun = dgamma, args = list(shape = 9, scale = 1),
linewidth = 0.9, color = "darkgreen") +
coord_cartesian(xlim = c(0, 20), ylim = c(0, 1)) +
labs(
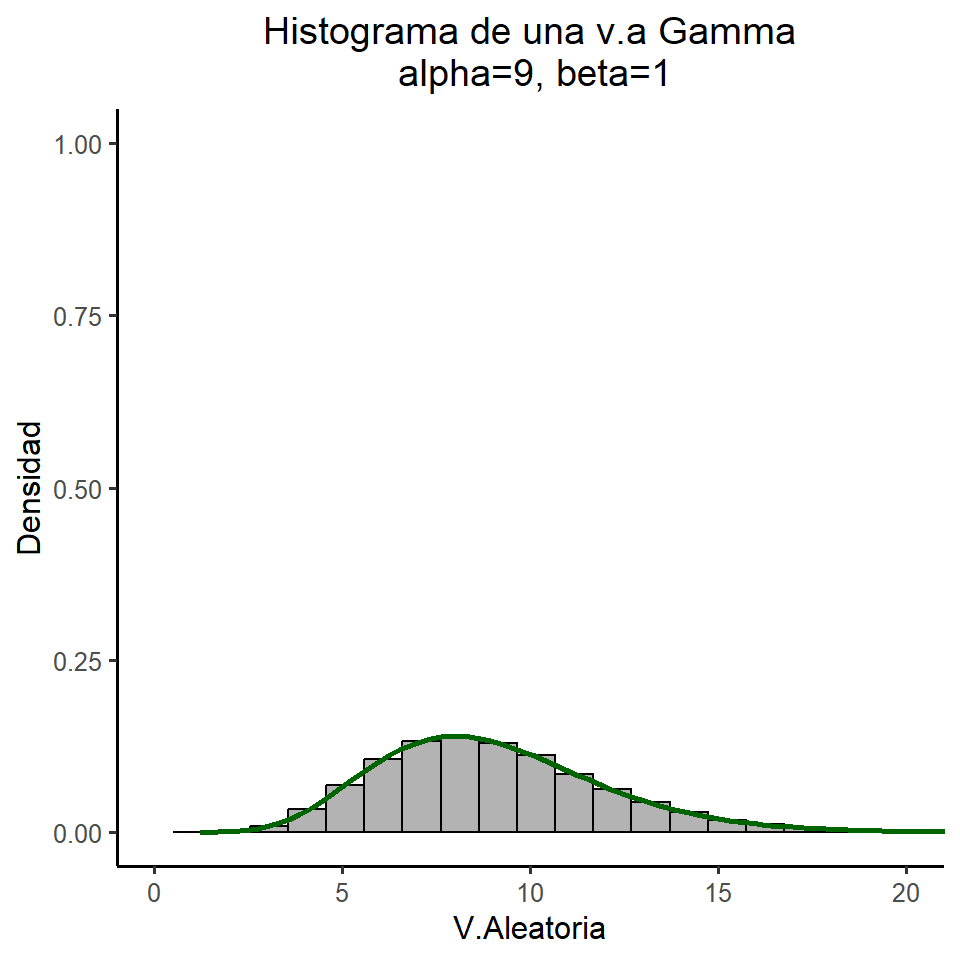
title = "Histograma de una v.a Gamma\ncon alpha=9, beta=1",
x = "V.Aleatoria", y = "Densidad"
) +
theme_classic(base_size = 12) +
theme(plot.title = element_text(hjust = 0.5))Distribución Gamma
library(ggplot2)
set.seed(123)
n <- 100000
df <- data.frame(vargamma = rgamma(n, shape = 9, scale = 1.5))
ggplot(df, aes(x = vargamma)) +
geom_histogram(aes(y = after_stat(density)),
bins = 30, fill = "grey70", color = "black") +
stat_function(fun = dgamma, args = list(shape = 9, scale = 1.5),
linewidth = 0.9, color = "darkgreen") +
coord_cartesian(xlim = c(0, 25), ylim = c(0, 1)) +
labs(
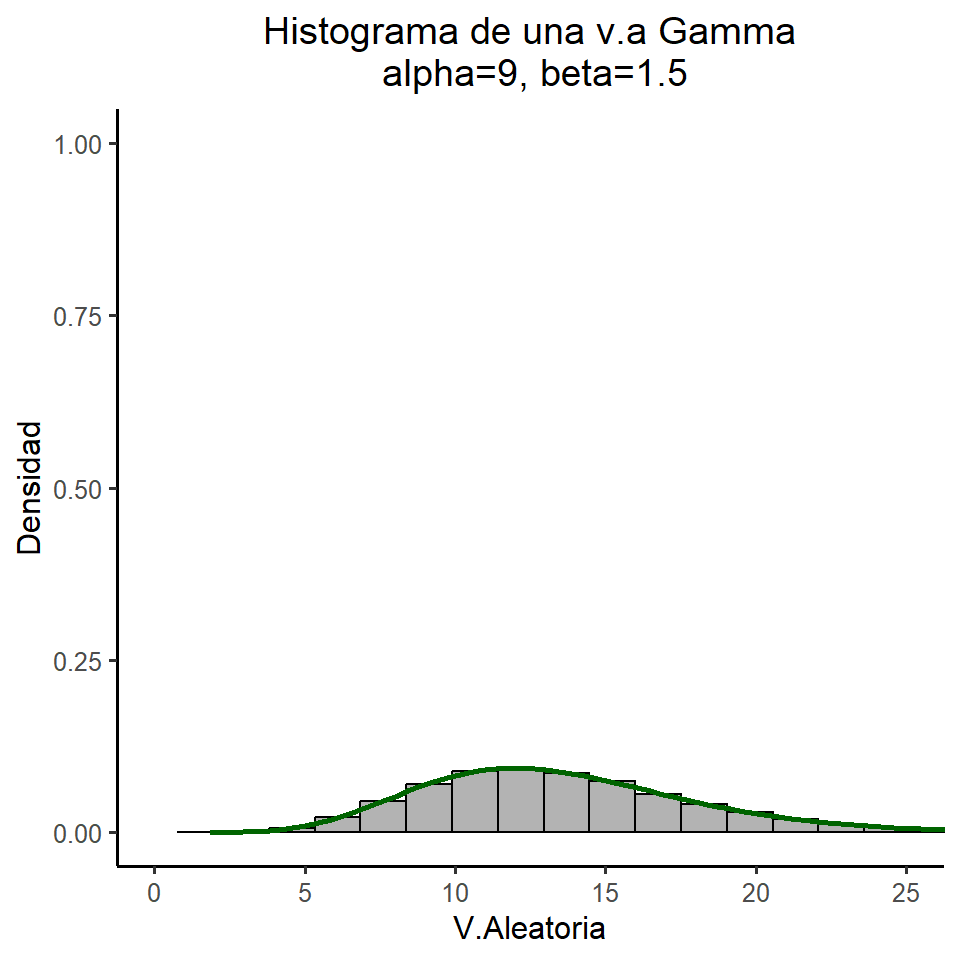
title = "Histograma de una v.a Gamma\ncon alpha=9, beta=1.5",
x = "V.Aleatoria", y = "Densidad"
) +
theme_classic(base_size = 12) +
theme(plot.title = element_text(hjust = 0.5))Distribución Gamma
Caso Especial
Cuando \(\alpha\) es un entero y \(\alpha \ne 1\) (una exponencial), podemos expresar la función de distribución de una variable aleatoria con distribución Gamma como una suma de ciertas probabilidades de Poisson.
Si \(\alpha\) no es entero y \(0 < a < b < \infty\), entonces esta integral no tiene una expresión cerrada:
\[ \int_a^b \dfrac{x^{\alpha - 1} e^{-x/\beta}}{\beta^{\alpha} \Gamma(\alpha)}\, dx \]
Por lo tanto, se requiere software estadístico para evaluar \(F_X(x)\).
Parámetros
La distribución Gamma tiene dos parámetros:
- \(\alpha\) (shape = forma)
- \(\beta\) (scale = escala)
Distribución Gamma
Si \(X\) es una variable aleatoria distribuida como Gamma con parámetros \(\alpha\) y \(\beta\), entonces:
\[ E(X) = \alpha \beta, \quad \text{y} \quad Var(X) = \alpha \beta^2. \]
Prueba
\[ E(X) = \int_{-\infty}^{\infty} x f(x)\,dx = \int_{0}^{\infty} x \, \dfrac{x^{\alpha - 1} e^{-x/\beta}}{\beta^{\alpha} \Gamma(\alpha)} \, dx \]
Sabemos que:
\[ \int_{0}^{\infty} \dfrac{x^{\alpha - 1} e^{-x/\beta}}{\beta^{\alpha} \Gamma(\alpha)} \, dx = 1 \;\; \Rightarrow \;\; \int_{0}^{\infty} x^{\alpha - 1} e^{-x/\beta} \, dx = \beta^{\alpha} \Gamma(\alpha) \]
\[ E(X) = \int_{0}^{\infty} x \, \dfrac{x^{\alpha - 1} e^{-x/\beta}}{\beta^{\alpha}\Gamma(\alpha)} \, dx = \dfrac{1}{\beta^{\alpha}\Gamma(\alpha)} \int_{0}^{\infty} x^{\alpha} e^{-x/\beta} \, dx \]
Distribución Gamma
\[ = \dfrac{\beta^{\alpha + 1} \Gamma(\alpha + 1)}{\beta^{\alpha}\Gamma(\alpha)} = \dfrac{\beta \alpha \Gamma(\alpha)}{\Gamma(\alpha)} = \alpha \beta \]
De la misma manera:
\[ E(X^2) = \int_{-\infty}^{\infty} x^2 f(x)\,dx = \int_{0}^{\infty} x^2 \, \dfrac{x^{\alpha - 1} e^{-x/\beta}}{\beta^{\alpha}\Gamma(\alpha)} \, dx = \dfrac{1}{\beta^{\alpha}\Gamma(\alpha)} \int_{0}^{\infty} x^{\alpha + 1} e^{-x/\beta} \, dx \]
\[ = \dfrac{\beta^{\alpha + 2} \Gamma(\alpha + 2)}{\beta^{\alpha}\Gamma(\alpha)} = \dfrac{\beta^2 (\alpha + 1)\alpha \Gamma(\alpha)}{\Gamma(\alpha)} = \alpha(\alpha + 1)\beta^2 \]
Por lo tanto:
\[ Var(X) = E(X^2) - [E(X)]^2 = \alpha(\alpha + 1)\beta^2 - \alpha^2\beta^2 = \alpha\beta^2 \]
Dos casos especiales de la Gamma
Chi Cuadrada
Sea \(\nu\) un entero positivo. Se dice que una variable aleatoria \(X\) tiene distribución Ji-cuadrada \(\chi^2\) con \(\nu\) grados de libertad si y solo si
\(X\) es una variable aleatoria con distribución Gamma con parámetros \(\alpha = \nu/2\) y \(\beta = 2\).
Esperanza y Varianza de una \(\chi^2\)
Si \(X\) es una variable aleatoria \(\chi^2\) con \(\nu\) grados de libertad, entonces:
\[ \mu = E(X) = \nu, \quad \sigma^2 = V(X) = 2\nu \]
Prueba: Ejercicio.
!!En casi todos los textos de estadística se pueden ver tablas que dan probabilidades asociadas con distribuciones \(\chi^2\). Además si \(X\) tiene una distribución \(Gamma(a = \frac{n}{2}, \beta)\), para algún entero \(n\) entonces \(Y = \frac{2X}{\beta}\) tiene una distribución \(\chi^2\) con \(n\) grados de libertad.
Dos casos especiales de la Gamma
Exponencial:
Se dice que una variable aleatoria \(X\) tiene una distribución exponencial con parámetro \(\beta > 0\) si y sólo si la función de densidad de \(X\) es:
\[ f_X(x) = \begin{cases} \dfrac{1}{\beta} e^{-x/\beta}, & 0 \le x < \infty, \\[6pt] 0, & \text{en cualquier otro punto.} \end{cases} \]
!!La función de densidad exponencial a menudo es de ayuda para modelar la vida útil de componentes electrónicos.
Esperanza y Varianza de una Exponencial
Si \(X\) es una variable aleatoria exponencial con parámetro \(\lambda\) entonces:
\[ \mu = E(X) = \lambda, \quad \sigma^2 = V(X) = \lambda^2 \]
Prueba: Ejercicio.
Ejercicio
Suponga que \(X\) tiene una función de densidad de probabilidad exponencial. Demuestre que, si \(a > 0\) y \(b > 0\),
\[\small P(X > a + b \mid X > a) = P(X > b) \]
Solución
\[\small P(X > a + b \mid X > a) = \dfrac{P(X > a + b, X > a)}{P(X > a)} = \dfrac{P(X > a + b)}{P(X > a)} \]
\[\small P(X > a + b) = \int_{a + b}^{\infty} \dfrac{1}{\beta} e^{-x/\beta}\,dx = e^{-(a+b)/\beta} \]
\[\small P(X > a) = \int_{a}^{\infty} \dfrac{1}{\beta} e^{-x/\beta}\,dx = e^{-a/\beta} \]
\[\small P(X > a + b \mid X > a) = \dfrac{e^{-(a+b)/\beta}}{e^{-a/\beta}} = e^{-b/\beta} = P(X > b) \]
\(\tiny \text{Esta propiedad se conoce como la propiedad sin memoria ya que la probabilidad de que el evento ocurra después de un tiempo adicional $b$ no depende del tiempo transcurrido $a$.}\)
Ejercicios
La magnitud de temblores en cierta región se modela con una distribución exponencial de media \(2.4\) (\(\beta=2.4\)). Calcule:
a) Probabilidad de que un temblor tenga una magnitud mayor a 3.0
\[\small P(X>3)=1-F(3)=1-\!\int_{0}^{3}\frac{1}{\beta}e^{-x/\beta}\,dx =1-(1-e^{-3/\beta})=e^{-3/\beta}. \]
\[\small P(X>3)=e^{-3/2.4}\approx 0.2865048. \]
b) Probabilidad de que un temblor tenga una magnitud entre 2.0 y 3.0
\[\small P(2<X<3)=F(3)-F(2)=(1-e^{-3/\beta})-(1-e^{-2/\beta}) = 0.1480934. \]
Distribución Beta
Se dice que una variable aleatoria \(X\) tiene una distribución Beta con parámetros \(\alpha>0\) y \(\beta>0\) si y sólo si su función de densidad es:
\[ f_X(x)= \begin{cases} \dfrac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}, & 0 \le x \le 1,\\[6pt] 0, & \text{en cualquier otro punto.} \end{cases} \]
con
\[ B(\alpha,\beta)=\int_{0}^{1} x^{\alpha-1}(1-x)^{\beta-1}\,dx = \dfrac{\Gamma(\alpha)\,\Gamma(\beta)}{\Gamma(\alpha+\beta)}. \]
La función de densidad beta es una función de densidad de dos parámetros definida sobre el intervalo cerrado \(0 \le x \le 1\). Frecuentemente se usa como modelo para proporciones, por ejemplo como la proporción de impurezas en un producto químico o la proporción de tiempo que una máquina está en reparación.
Distribución Beta
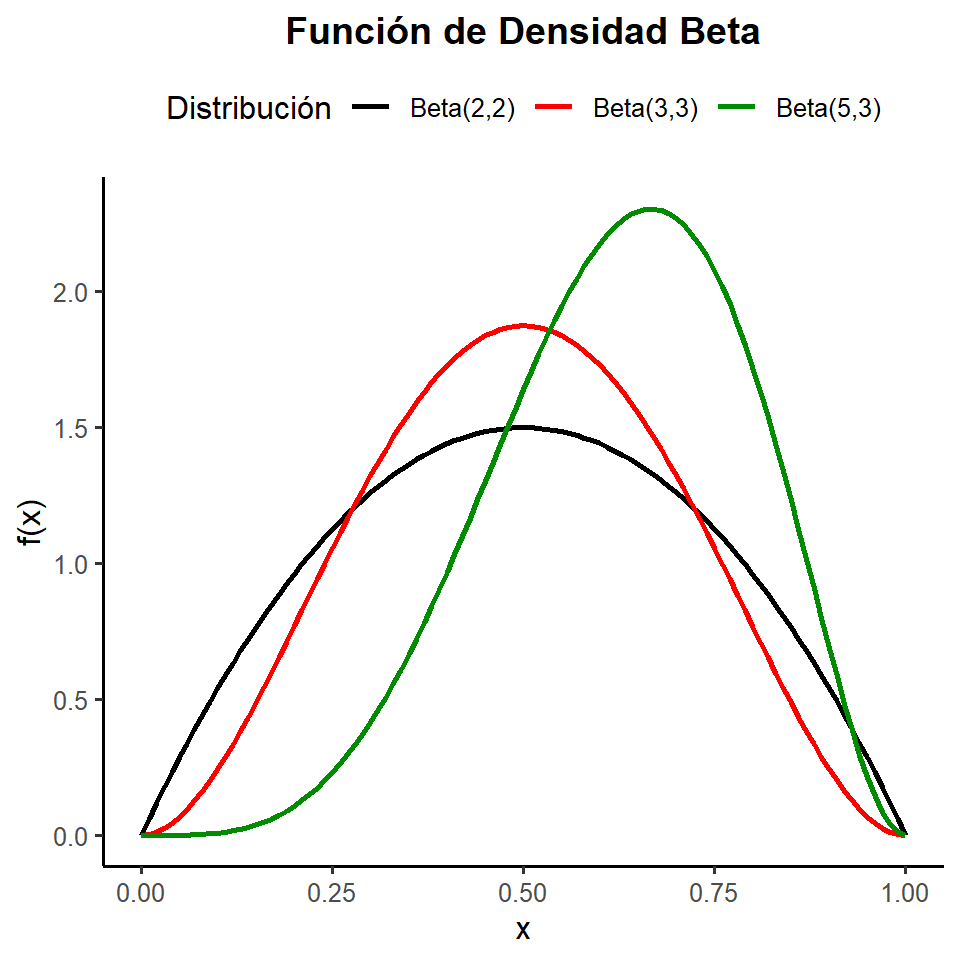
De igual forma de la función de densidad va a depender de los valores de \(\alpha\) y \(\beta\).
library(ggplot2)
x <- seq(0, 1, 0.01)
df <- data.frame(
x = rep(x, 3),
densidad = c(dbeta(x, 5, 3), dbeta(x, 3, 3), dbeta(x, 2, 2)),
distribucion = factor(c(
rep("Beta(5,3)", length(x)),
rep("Beta(3,3)", length(x)),
rep("Beta(2,2)", length(x))
))
)
ggplot(df, aes(x = x, y = densidad, color = distribucion)) +
geom_line(linewidth = 1) +
labs(
title = "Función de Densidad Beta",
x = "x",
y = "f(x)",
color = "Distribución"
) +
scale_color_manual(values = c("black", "red", "green4")) +
theme_classic(base_size = 12) +
theme(
plot.title = element_text(hjust = 0.5, face = "bold"),
legend.position = "top"
)Distribución Beta
Observe que definir \(x\) en el intervalo \(0 \le x \le 1\) no restringe el uso de la distribución Beta.
Si \(c \le x \le d\), entonces se puede definir una nueva variable:
\(x^* = \dfrac{x - c}{d - c}\) de modo que \(0 \le x^* \le 1\).
Cambio de escala: La función de densidad Beta puede aplicarse a una variable aleatoria definida en el intervalo \(c \le x \le d\) mediante traslación y cambio de escala.
Función de distribución acumulativa
La función de distribución acumulativa (FDA) para la variable Beta se denomina función Beta incompleta y se denota por:
\[ F(x) = \int_{0}^{x} \dfrac{t^{\alpha - 1}(1 - t)^{\beta - 1}}{B(\alpha, \beta)}\,dt = I_x(\alpha, \beta) \]
Distribución Beta
Relación con la distribución binomial
Cuando \(\alpha\) y \(\beta\) son enteros positivos, la función \(I_x(\alpha, \beta)\) está relacionada con la función de probabilidad binomial. Es posible usar integración por partes para demostrar que, si \(0 < x < 1\) y \(\alpha, \beta\) son enteros, entonces:
\[ F(x) = \int_{0}^{x} \dfrac{t^{\alpha - 1}(1 - t)^{\beta - 1}}{B(\alpha, \beta)}\,dt = \sum_{i = \alpha}^{n} \binom{n}{i} x^{i}(1 - x)^{n - i}, \]
donde: \(n = \alpha + \beta - 1\)
La suma del lado derecho representa la suma de probabilidades asociadas a una variable aleatoria binomial con:
\[ n = \alpha + \beta - 1, \quad p = x. \]
Distribución Beta
Si \(X\) es una variable aleatoria Beta con parámetros \(\alpha > 0\) y \(\beta > 0\), entonces:
\[\small \mu = E(X) = \dfrac{\alpha}{\alpha + \beta} \quad \text{y} \quad \sigma^2 = V(X) = \dfrac{\alpha \beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)}. \]
Prueba - Utilizamos la definición de \(E(X)\):
\[\small E(X) = \int_{-\infty}^{\infty} x f(x)\,dx = \int_{0}^{1} x \left[ \dfrac{x^{\alpha - 1}(1 - x)^{\beta - 1}}{B(\alpha, \beta)} \right] dx = \dfrac{1}{B(\alpha, \beta)} \int_{0}^{1} x^{\alpha}(1 - x)^{\beta - 1}\,dx \]
Sabemos que:
\[\small \dfrac{B(\alpha + 1, \beta)}{B(\alpha, \beta)} = \dfrac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} \cdot \dfrac{\Gamma(\alpha + 1)\Gamma(\beta)}{\Gamma(\alpha + \beta + 1)} = \dfrac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} \cdot \dfrac{\alpha \Gamma(\alpha)\Gamma(\beta)}{(\alpha + \beta)\Gamma(\alpha + \beta)} = \dfrac{\alpha}{\alpha + \beta} \]
Por tanto:
\[\small E(X) = \dfrac{\alpha}{\alpha + \beta} \]
Ejercicios: (Libro Wackerly, Mendenhall - Capítulo 4)
Uniforme: 4.39 - 4.57
Normal: 4.58 - 4.80
Gamma: 4.81 - 4.112
Beta: 4.136 - 4.145