Variable Aleatoria
Variable Aleatoria continua
Definición.
\(X\) es una variable aleatoria continua si posee una función no negativa \(f_X:R \Rightarrow R\) definida e integrable en \(R\), tal que para cualesquiera \(a,b\in R\) se cumple:
\[ P(a \le X \le b)=\int_{a}^{b} f_X(x)\,dx \]
\[ P(X \le b)=\int_{-\infty}^{b} f_X(x)\,dx \]
\[ P(X \ge a)=\int_{a}^{+\infty} f_X(x)\,dx \]
Usualmente a \(f_X\) se le llama función de densidad de probabilidad de \(X\).
Variable Aleatoria continua
Propiedades de la densidad
Sea \(f_X:R\to R\). Es una densidad de una v.a. continua \(X\) si y solo si:
\[f_X(x)\ge 0,\ \forall x\in R\]
\[\int_{-\infty}^{+\infty} f_X(x)\,dx = 1\]
Variable Aleatoria continua
Función de distribución acumulada (**)
Sea \(X\) una v.a.c. con densidad \(f_X\). La función \(F_X:R \Rightarrow R\) dada por
\[ F_X(x)=P(X\le x)=\int_{-\infty}^{x} f_X(t)\,dt \]
se llama función de distribución acumulada (o simplemente función de distribución).
Variable Aleatoria continua
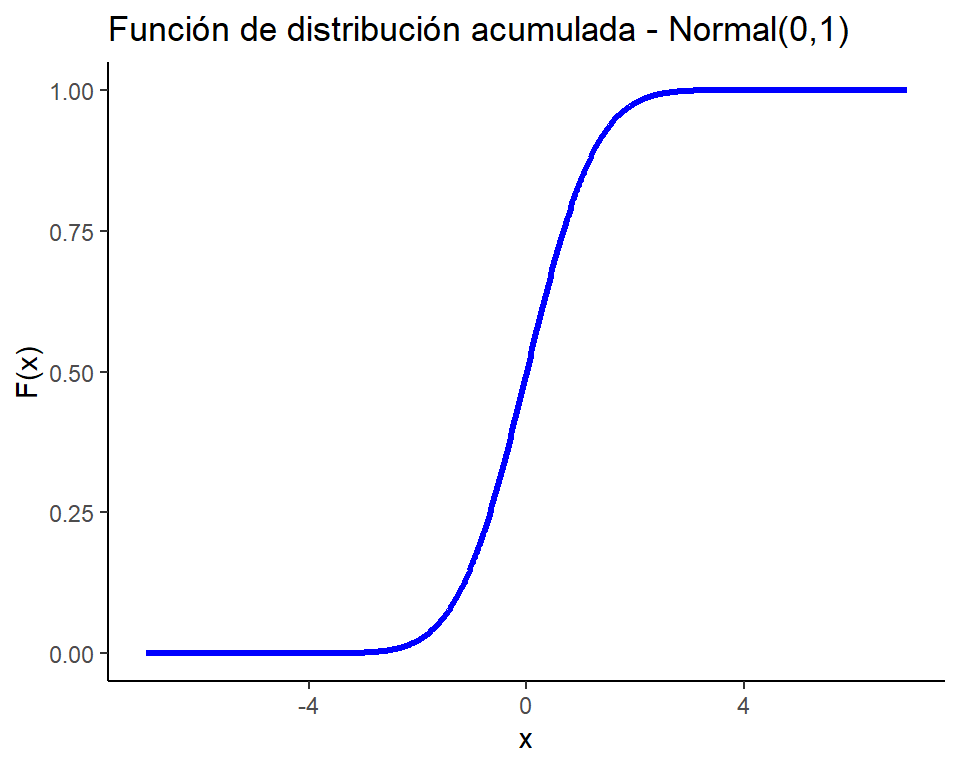
Una variable aleatoria \(Y\) con función de distribución \(F(y)\) se dice que es continua si \(F(y)\) es continua, para \(- \infty < y < \infty\)
Variable Aleatoria continua
Propiedades de la función de distribución:
- \(F_X(x)\ge 0,\ \forall x\in R\)
- Si \(x\le y\), entonces \(F_X(x)\le F_X(y)\) (es creciente).
- \(P(X> x)=1-P(X\le x),\quad \forall x\in R\)
- \(P(a\le X\le b)=\int_{a}^{b} f_X(x)\,dx\)
- \(\lim_{x\to -\infty}F_X(x)=0,\quad \lim_{x\to +\infty}F_X(x)=1\)
Variable aleatoria continua
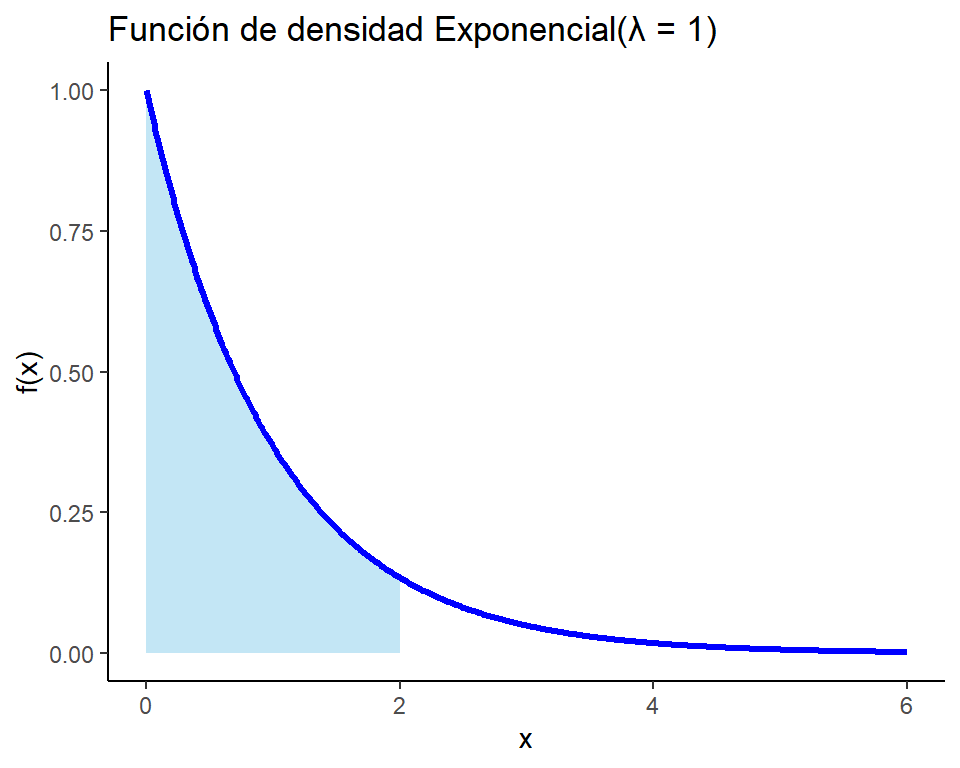
La función de distribución \(F(y)\) evaluada en un punto \(y_o\) equivale al área de la función de densidad \(f(y)\) hasta el punto \(y_o\).
Para el caso de una función de densidad exponencial con \(\lambda = 1\). Se tiene que \(F(y=2)\) es la siguiente área sombreada.
Variable aleatoria continua
Definición función de densidad:
Sea \(F(y)\) la función de distribución para una variable aleatoria continua \(Y\).
Entonces la función densidad \(f(y)\), dada por
\[ f(y)=\frac{dF(y)}{dy}=F'(y), \]
siempre que exista la derivada, se denomina función de densidad de probabilidad para la variable aleatoria \(Y\).
Se deduce que \(F(y)\) se puede escribir como
\[ F(y)=\int_{-\infty}^{y} f(t)\,dt, \]
donde \(f(\cdot)\) es la función de densidad de probabilidad y \(t\) se usa como la variable de integración.
Variable aleatoria continua
Ejemplo: Función de densidad y distribución
Sea \(Y\) una variable aleatoria continua con función de densidad de probabilidad dada por
\[ f(y)= \begin{cases} 3y^2, & 0 \le y \le 1, \\ 0, & \text{en otro caso}. \end{cases} \]
Ejercicios:
1. Encuentre \(F(y)\).
2. Grafique \(f(y)\) y \(F(y)\).
Variable aleatoria continua
Ahora que conocemos la definición de \(f(x)\) y \(F(x)\), podemos estudiar otras maneras de describir la función, como por ejemplo las medidas de centralidad: moda, mediana y media, además de otros percentiles.
Valor Esperado de VA. Continua:
El valor esperado de una variable aleatoria continua \(Y\) es
\[ E(Y) = \int_{-\infty}^{\infty} y f(y)\,dy, \]
siempre que exista la integral.
Técnicamente, se dice que \(E(Y)\) existe si
\[ E(Y) = \int_{-\infty}^{\infty} |y| f(y)\,dy < \infty. \]
Variable aleatoria continua
Teorema: Esperanza de una Transformación
Sea \(g(Y)\) una función de \(Y\); entonces el valor esperado de \(g(Y)\) está dado por
\[ E[g(Y)] = \int_{-\infty}^{\infty} g(y)\, f(y)\,dy < \infty, \]
siempre que exista la integral.
Variable aleatoria continua
Propiedades de la Esperanza*
Sea \(c\) una constante y sean \(g(Y),\, g_1(Y),\, g_2(Y),\,\ldots,\, g_k(Y)\) funciones de una variable aleatoria continua \(Y\).
Entonces se cumplen los siguientes resultados:
- \(E(c) = c\)
- \(E \left [ g(Y) \right ] = c\,E[g(Y)]\)
- \(E \left [g_1(Y) + g_2(Y) + \cdots + g_k(Y) \right ] = E[g_1(Y)] + E[g_2(Y)] + \cdots + E[g_k(Y)]\)
*se emplea para determinar \(E[g(X)]\) de una v.a. \(X\) cuando se conoce la distribución de \(X\), pero no se conoce la de \(g(X)\).
Variable aleatoria continua
Varianza
Usando los teoremas anteriores, ¿cómo definimos la varianza?
\[ \operatorname{Var}(Y) = E[(Y-\mu)^2] = E(Y^2 - 2Y\mu + \mu^2) = E(Y^2) - 2\mu E(Y) + \mu^2 \]
\[ \operatorname{Var}(Y) = E(Y^2) - \mu^2 \]
Variable aleatoria continua
Ejemplo: Supongamos que
\[ f(y) = \begin{cases} \frac{3}{8} y^2, & 0 \leq y \leq 2, \\ 0, & \text{en otro caso}, \end{cases} \]
es una función de densidad válida.
Si la variable aleatoria \(Y\) tiene esta densidad, encuentre:
- \(E(Y)\)
- \(\operatorname{Var}(Y)\).
Variable aleatoria continua
Cálculo de \(E(Y)\)
\[ E(Y) = \int_{-\infty}^{\infty} y f(y)\,dy = \int_0^2 y \,\frac{3}{8} y^2 \, dy = \int_0^2 \frac{3}{8} y^3 \, dy = \frac{3}{8} \left[\frac{y^4}{4}\right]_0^2 = 1.5 \]
Cálculo de \(E(Y^2)\)
\[ E(Y^2) = \int_{-\infty}^{\infty} y^2 f(y)\,dy = \int_0^2 y^2 \,\frac{3}{8} y^2 \, dy = \int_0^2 \frac{3}{8} y^4 \, dy = \frac{3}{8} \left[\frac{y^5}{5}\right]_0^2 = 2.4 \]
Cálculo de la varianza
\[ \operatorname{Var}(Y) = E(Y^2) - \mu^2 = 2.4 - (1.5)^2 = 0.15 \]
Variable aleatoria continua
Denotemos con \(Y\) cualquier variable aleatoria continua.
Si \(0 < p < 1\), la mediana es el \(0.50\)-ésimo cuantil de \(Y\), denotado por \(\varphi_{0.5}\), y es el mínimo valor tal que
\[ F(\varphi_{0.5}) = P(Y \leq \varphi_{0.5}) = 0.5. \]
Algunos prefieren llamar \(\varphi_{0.5}\) al 50-ésimo percentil de \(Y\).
Variable aleatoria continua
Supongamos la misma función
\[ f(y) = \begin{cases} \frac{3}{8} y^2, & 0 \leq y \leq 2, \\ 0, & \text{en otro caso}. \end{cases} \]
Si la variable aleatoria \(Y\) tiene esta densidad, encuentre \(F(\varphi_{0.5})\).
Desarrollo
\[ F(\varphi_{0.5}) = P(Y \leq \varphi_{0.5}) = 0.50 \]
\[ P(Y \leq \varphi_{0.5}) = \int_{-\infty}^{\varphi_{0.5}} f(y)\,dy = \int_0^{\varphi_{0.5}} \frac{3}{8} y^2 \, dy = \frac{3}{8}\left[\frac{y^3}{3}\right]_0^{\varphi_{0.5}} = \frac{(\varphi_{0.5})^3}{8} \]
Resultado
\[ (\varphi_{0.5})^3 = 8 \cdot 0.50 \Rightarrow \varphi_{0.5} = \sqrt[3]{8 \cdot 0.50} \approx 1.5874 \]
Ejercicio
Sea \(X\) una variable aleatoria con densidad
\[ \small f_X(x)= \begin{cases} \frac{k}{9}, & 1\le x\le 2,\\\\ \frac{kx}{6}-1, & 2< x\le 3,\\\\ 0, & \text{en otro caso.} \end{cases} \]
a) Determine el valor de \(k\).
b) Calcule \(\small P\!\left(\dfrac{3}{2} < X < \dfrac{5}{2}\right)\).
c) Obtenga \(\small F_X(x)\).
d) Calcule \(\small E(X)\) y \(\small \operatorname{Var}(X)\).
e) Determine el cuantil \(\small \varphi_{0.75}\).
Ejercicio
Sea \(X\) una v.a. con función de distribución acumulada
\[ \small F_X(x)= \begin{cases} 0, & x<0,\\\\ \frac{x^2}{2}, & 0\le x\le 1,\\\\ -\dfrac{x^2}{2}+2x-1, & 1< x\le 2,\\\\ 1, & x>2. \end{cases} \]
a) Encuentre la densidad \(\small f_X(x)\).
b) Calcule \(\small P\!\left(\frac{3}{4}<X<\frac{5}{3}\right)\).
c) Calcule \(\small E(X)\) y \(\small \operatorname{Var}(X)\).
d) Determine el cuantil \(\small \varphi_{0.65}\).
Variable aleatoria continua
Sea \(Y\) una variable aleatoria continua con función de densidad
\[ f(y)= \begin{cases} k\,y(1-y), & 0 \le y \le 1,\\ 0, & \text{en otro caso}. \end{cases} \]
Responda:
Encuentre el valor de \(k\) que hace a \(f(y)\) una densidad de probabilidad.
Calcule \(P(0.4 \le Y \le 1)\).
Calcule \(P(0.4 \le Y < 1)\).
Calcule \(P(Y \le 0.4 \mid Y \le 0.8)\).
Calcule \(P(Y < 0.4 \mid Y < 0.8)\).
Encuentre el cuantil 95, es decir, \(\varphi_{0.95}\).
Variable aleatoria continua
Suponga que \(Y\) posee la función de densidad
\[ f(y)= \begin{cases} c\,y, & 0 \le y \le 2,\\ 0, & \text{en otro caso}. \end{cases} \]
Responda:
Encuentre el valor de \(c\) que hace a \(f(y)\) una función de densidad de probabilidad.
Encuentre \(F(y)\).
Grafique \(f(y)\) y \(F(y)\).